Introduzione al Teorema di Bayes: Bayesian
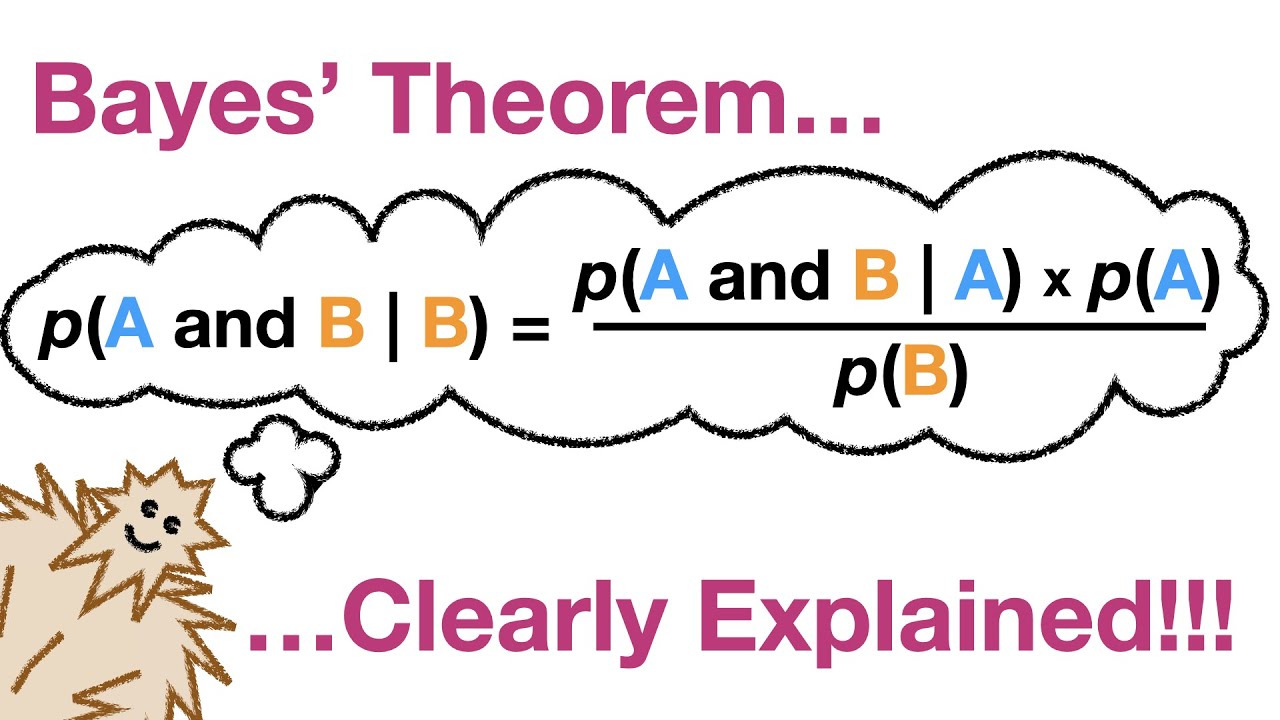
Il teorema di Bayes è uno strumento fondamentale nella probabilità e nell’inferenza statistica. Ci aiuta a capire come aggiornare le nostre credenze sulla base di nuove informazioni. In termini semplici, il teorema di Bayes ci dice come la probabilità di un evento cambia quando abbiamo nuove prove a disposizione.
Per illustrare questo concetto, immaginiamo di avere un test medico per una certa malattia. Il test non è perfetto, può dare falsi positivi e falsi negativi. Supponiamo che il test abbia una sensibilità del 90% (significa che il 90% delle persone malate otterrà un risultato positivo al test) e una specificità del 95% (significa che il 95% delle persone sane otterrà un risultato negativo al test). Ora, supponiamo che una persona casuale abbia un risultato positivo al test. Qual è la probabilità che questa persona sia effettivamente malata?
Il teorema di Bayes ci aiuta a rispondere a questa domanda. Ci dice che la probabilità che una persona sia malata dato un risultato positivo al test è uguale alla probabilità di ottenere un risultato positivo al test dato che la persona è malata, moltiplicata per la probabilità che la persona sia malata, il tutto diviso per la probabilità di ottenere un risultato positivo al test.
Formulazione Matematica del Teorema di Bayes
Il teorema di Bayes può essere espresso matematicamente come segue:
P(A|B) = [P(B|A) * P(A)] / P(B)
Dove:
* P(A|B) è la probabilità dell’evento A dato che l’evento B è avvenuto.
* P(B|A) è la probabilità dell’evento B dato che l’evento A è avvenuto.
* P(A) è la probabilità dell’evento A.
* P(B) è la probabilità dell’evento B.
Nel nostro esempio del test medico, A rappresenterebbe l’evento “essere malato” e B rappresenterebbe l’evento “ottenere un risultato positivo al test”.
Importanza del Teorema di Bayes
Il teorema di Bayes è uno strumento potente che ha numerose applicazioni in vari campi, tra cui:
* Medicina: per diagnosticare le malattie e valutare l’efficacia dei trattamenti.
* Ingegneria: per analizzare i dati e migliorare i sistemi.
* Finanza: per prevedere i movimenti del mercato e gestire i rischi.
* Scienze sociali: per studiare i comportamenti umani e le opinioni pubbliche.
Il teorema di Bayes ci permette di aggiornare le nostre credenze in modo razionale e oggettivo, tenendo conto di nuove informazioni. È uno strumento fondamentale per prendere decisioni informate in situazioni di incertezza.
Applicazioni del Teorema di Bayes

Il Teorema di Bayes è uno strumento potente che ha trovato applicazione in una vasta gamma di campi, dalla medicina alla finanza, dall’intelligenza artificiale all’analisi dei dati. Questo teorema fornisce un metodo per aggiornare le nostre credenze sulla base di nuove evidenze, consentendoci di prendere decisioni più informate in situazioni di incertezza.
Applicazioni del Teorema di Bayes in diversi campi, Bayesian
Il Teorema di Bayes è un’arma potente che può essere applicata in vari settori, tra cui:
- Medicina: In ambito medico, il Teorema di Bayes è utilizzato per diagnosticare malattie, valutare l’efficacia di trattamenti e prevedere il rischio di sviluppare determinate condizioni. Ad esempio, un medico può utilizzare il teorema di Bayes per calcolare la probabilità che un paziente abbia una specifica malattia, date le sue caratteristiche cliniche e i risultati dei test.
- Finanza: Il Teorema di Bayes è impiegato nella gestione del rischio e nella previsione del mercato finanziario. Gli analisti finanziari possono utilizzare questo teorema per valutare la probabilità di un evento specifico, come un’aumento del prezzo di un’azione o un calo del mercato azionario.
- Intelligenza artificiale: L’intelligenza artificiale (IA) si basa ampiamente sul Teorema di Bayes per lo sviluppo di algoritmi di apprendimento automatico. Ad esempio, i filtri antispam utilizzano il teorema di Bayes per classificare i messaggi come spam o non spam, mentre i sistemi di riconoscimento vocale si basano su questo teorema per comprendere il linguaggio umano.
- Analisi dei dati: Il Teorema di Bayes è un pilastro fondamentale dell’analisi dei dati, permettendo di individuare modelli e relazioni nascoste in grandi set di dati. Questo teorema è utilizzato in diversi ambiti, come la previsione delle vendite, l’analisi del comportamento dei clienti e la scoperta di nuove conoscenze.
Confronto delle applicazioni del Teorema di Bayes
Ecco una tabella che confronta le diverse applicazioni del Teorema di Bayes, evidenziando i vantaggi e gli svantaggi di ciascuna:
| Campo | Vantaggi | Svantaggi |
|---|---|---|
| Medicina | Migliora la precisione diagnostica, aiuta a prendere decisioni informate sui trattamenti, consente di valutare il rischio di sviluppare determinate condizioni. | Richiede dati accurati e affidabili, può essere complesso da applicare in situazioni con molti fattori da considerare. |
| Finanza | Permette di valutare il rischio in modo più accurato, aiuta a prendere decisioni di investimento più informate, consente di prevedere l’andamento del mercato finanziario. | Dipende da modelli e previsioni che possono essere imprecise, può essere influenzato da fattori esterni imprevedibili. |
| Intelligenza artificiale | Consente di sviluppare algoritmi di apprendimento automatico più efficienti, migliora la capacità di classificazione e previsione, aiuta a comprendere il linguaggio umano. | Richiede grandi quantità di dati per l’addestramento, può essere sensibile a errori nei dati di input. |
| Analisi dei dati | Aiuta a individuare modelli e relazioni nascoste nei dati, consente di prevedere eventi futuri, facilita la scoperta di nuove conoscenze. | Può essere complesso da applicare a grandi set di dati, richiede competenze specifiche nell’analisi dei dati. |
Esempi concreti di applicazioni del Teorema di Bayes
Il Teorema di Bayes viene utilizzato in diverse situazioni reali, tra cui:
- Diagnosi medica: Un medico utilizza il teorema di Bayes per calcolare la probabilità che un paziente abbia una specifica malattia, date le sue caratteristiche cliniche e i risultati dei test. Ad esempio, se un paziente presenta sintomi di influenza e ha un test positivo per l’influenza, il medico può utilizzare il teorema di Bayes per calcolare la probabilità che il paziente abbia effettivamente l’influenza, tenendo conto della prevalenza dell’influenza nella popolazione e dell’accuratezza del test.
- Filtri antispam: I filtri antispam utilizzano il teorema di Bayes per classificare i messaggi come spam o non spam. Il sistema analizza le parole chiave, l’indirizzo del mittente e altri fattori per determinare la probabilità che un messaggio sia spam.
- Previsione del mercato azionario: Gli analisti finanziari possono utilizzare il teorema di Bayes per valutare la probabilità di un evento specifico, come un’aumento del prezzo di un’azione o un calo del mercato azionario. Ad esempio, possono analizzare i dati storici del mercato azionario, i dati economici e le notizie finanziarie per prevedere l’andamento del mercato azionario.
Concetti correlati al Teorema di Bayes

Il Teorema di Bayes è un potente strumento per l’aggiornamento delle credenze alla luce di nuove informazioni. Per comprenderlo appieno, è necessario familiarizzare con alcuni concetti fondamentali come la probabilità condizionata, la probabilità a priori e la probabilità a posteriori.
Probabilità condizionata, probabilità a priori e probabilità a posteriori
La probabilità condizionata è la probabilità di un evento che si verifica dato che un altro evento si è già verificato. Ad esempio, la probabilità che un paziente abbia la febbre dato che ha il raffreddore è la probabilità condizionata.
La probabilità a priori è la probabilità di un evento prima che si verifichino nuove informazioni. Ad esempio, la probabilità che un paziente abbia il raffreddore prima di qualsiasi test o osservazione è la probabilità a priori.
La probabilità a posteriori è la probabilità di un evento dopo che si sono verificate nuove informazioni. Ad esempio, la probabilità che un paziente abbia il raffreddore dopo che è stato riscontrato positivo al test per il raffreddore è la probabilità a posteriori.
Il Teorema di Bayes mette in relazione la probabilità a posteriori di un evento con la probabilità a priori e la probabilità condizionata.
Utilizzo del Teorema di Bayes per aggiornare le credenze
Il Teorema di Bayes può essere utilizzato per aggiornare le credenze alla luce di nuove informazioni. In sostanza, ci dice come cambiare la nostra convinzione iniziale su un evento (probabilità a priori) dopo aver osservato nuove prove (probabilità condizionata).
Ad esempio, supponiamo che un medico stia cercando di determinare se un paziente ha un’influenza. La probabilità a priori che un paziente abbia l’influenza è bassa. Tuttavia, se il paziente ha la febbre, la tosse e il mal di gola, il medico può aggiornare la sua convinzione sulla probabilità che il paziente abbia l’influenza.
Il Teorema di Bayes ci dice come calcolare la probabilità a posteriori che il paziente abbia l’influenza, tenendo conto della probabilità a priori e della probabilità condizionata di avere questi sintomi dato che ha l’influenza.
Confronto con altri approcci all’inferenza statistica
Il Teorema di Bayes è un approccio all’inferenza statistica che si basa sulla probabilità soggettiva. Questo è in contrasto con la statistica frequentista, che si basa sulla probabilità oggettiva.
La statistica frequentista si basa sul concetto di frequenza relativa. Ad esempio, la probabilità di ottenere testa lanciando una moneta è 0,5, perché in un numero infinito di lanci, si otterrebbe testa il 50% delle volte.
La statistica bayesiana, invece, si basa sulla probabilità soggettiva, che è la convinzione personale di un individuo sulla probabilità di un evento. Ad esempio, se un individuo crede che la probabilità di ottenere testa lanciando una moneta sia 0,6, questa è la sua probabilità soggettiva.
Il Teorema di Bayes è un potente strumento per l’aggiornamento delle credenze alla luce di nuove informazioni. È un approccio flessibile e intuitivo all’inferenza statistica che può essere applicato a una vasta gamma di problemi.
Bayesian methods, often employed in statistical analysis, rely on prior knowledge to inform future predictions. This approach, much like the concept of a “tycoon significato” tycoon significato , where influence and power are intertwined, highlights the importance of context and experience in shaping outcomes.
Bayesian analysis, by incorporating past data, allows for a more nuanced understanding of complex systems, ultimately leading to more accurate and informed decisions.
Bayesian statistics, with its emphasis on updating beliefs based on new evidence, can be applied to various fields, including the study of human relationships. For instance, understanding the influence of a spouse, such as Mike Lynch’s wife , on a person’s life can be approached through a Bayesian lens, considering prior beliefs and adjusting them based on observed data.
This approach can provide valuable insights into the dynamics of personal relationships and their impact on individuals’ decisions and actions.
